Introductio
In capitulo praecedenti demonstratum est condiciones mathematicas exactas pro viribus a fluidis quiescentibus exercitis facile obtineri posse. Hoc fit quia in hydrostatica solae vires pressionis simplices implicantur. Cum fluidum in motu consideratur, problema analysis statim fit multo difficilius. Non solum magnitudo et directio velocitatis particularum considerandae sunt, sed etiam est complexa viscositatis influentia quae vim scissoriam vel frictionalem inter particulas fluidi moventes et ad limites continentes efficit. Motus relativus qui inter diversa elementa corporis fluidi possibilis est facit ut pressione et vi scissoria inter unum punctum et alterum secundum condiciones fluxus valde varient. Propter complexitates cum phaenomeno fluxus coniunctas, accurata analysis mathematica tantum in paucis casibus, et ex prospectu machinali, nonnullis impracticabilibus, possibilis est. Ergo necesse est problemata fluxus solvere vel experimentando, vel per certas suppositiones simplificantes sufficientes ad solutionem theoreticam obtinendam. Duae rationes non se inter se excludunt, cum leges fundamentales mechanicae semper validae sint et permittant methodos partim theoreticas in pluribus casibus magni momenti adoptari. Etiam magni momenti est experimentaliter explorare quantum aberrationis a condicionibus veris ex analysi simpliciori resultans sit.
Frequentissima suppositio simplificans est fluidum ideale vel perfectum esse, ita effectus viscosos complicatos eliminans. Hoc est fundamentum hydrodynamicae classicae, rami mathematicae applicatae cui attentio a peritis eminentibus ut Stokes, Rayleigh, Rankine, Kelvin et Lamb venit. Sunt graviae limitationes in theoria classica innatae, sed cum aqua viscositatem relative humilem habeat, se gerit ut fluidum reale in multis condicionibus. Quapropter, hydrodynamica classica considerari potest ut fundamentum pretiosissimum ad studium proprietatum motus fluidi. Praesens caput dynamica fundamentali motus fluidi tractat et servit ut introductio fundamentalis ad capita sequentia quae problemata magis specifica in hydraulica ingeniaria civili occurrunt tractant. Tres aequationes fundamentales motus fluidi, scilicet aequationes continuitatis, Bernoulli et momenti, derivantur et earum significatio explicatur. Postea, limitationes theoriae classicae considerantur et modus agendi fluidi realis describitur. Fluidum incompressibile per totum assumitur.
Genera fluxus
Varia genera motus fluidorum sic classificari possunt:
1. Turbulens et laminaris
2. Rotationalis et irrotationalis
3. Stabilis et instabilis
4. Uniformis et non uniformis.
Antlia Cloacarum Submersibilis
Antliae fluxus axialis seriei MVS Antliae fluxus mixti seriei AVS (fluxus axialis verticalis et antlia submersibilis fluxus mixti) sunt productiones modernae, feliciter designatae per usum technologiae externae modernae. Capacitas antliarum novarum 20% maior est quam veterum. Efficacia 3~5% altior est quam veterum.

Fluxus turbulentus et laminaris.
Haec vocabula naturam physicam fluxus describunt.
In fluxu turbulento, progressio particularum fluidi irregularis est et commutatio positionum quasi fortuita fit. Singulae particulae fluctuationibus velocitatum transversarum obnoxiae sunt, ita ut motus sit vorticosus et sinuosus potius quam rectilineus. Si tinctura in certo loco iniicitur, celeriter per fluxum diffundetur. In casu fluxus turbulenti in tubo, exempli gratia, instantanea adnotatio velocitatis in sectione distributionem approximatam revelaret, ut in Figura 1(a) monstratur. Velocitas stabilis, qualis instrumentis mensurae normalibus adnotaretur, linea punctata indicatur, et apparet fluxum turbulentum velocitate fluctuante instabili superimposita mediae stabili temporali notari.
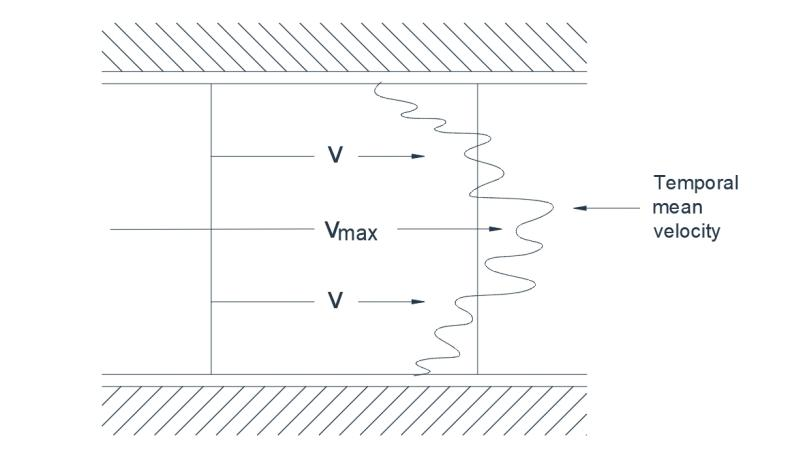
Fig. 1(a) Fluxus turbulentus
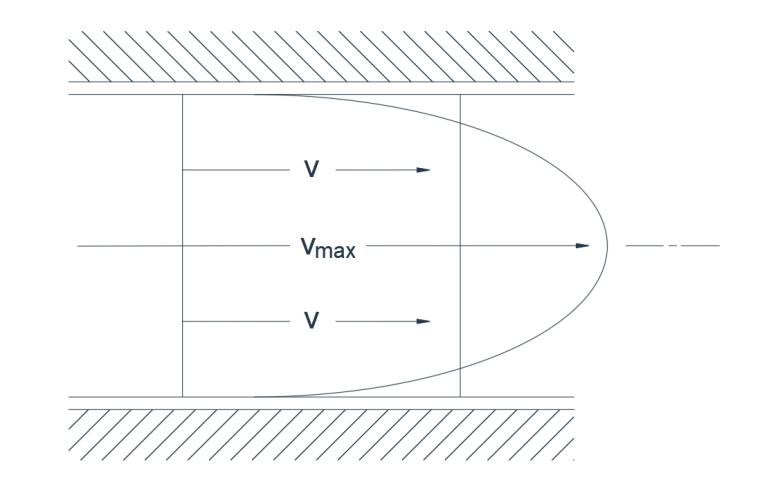
Fig. 1(b) Fluxus laminaris
In fluxu laminari omnes particulae fluidi per vias parallelas procedunt, neque ulla est pars transversalis velocitatis. Progressio ordinata talis est ut quaeque particula exacte viam particulae praecedentis sequatur sine ulla deviatione. Ita tenue filamentum tincturae manebit tale sine diffusione. Multo maior est gradiens velocitatis transversalis in fluxu laminari (Fig. 1b) quam in fluxu turbulento. Exempli gratia, pro tubo, ratio velocitatis mediae V et velocitatis maximae V max est 0,5 cum fluxu turbulento et 0,05 cum fluxu laminari.
Fluxus laminaris cum velocitatibus parvis et fluidis viscosis et pigris coniungitur. In hydraulicis fistularum et canalium apertorum, velocitates fere semper satis altae sunt ut fluxum turbulentum praestent, quamquam tenue stratum laminare prope limitem solidum permanet. Leges fluxus laminaris plene intelleguntur, et pro condicionibus limitum simplicibus distributio velocitatis mathematice analysari potest. Propter naturam suam irregularem et pulsantem, fluxus turbulentus tractationem mathematicam rigorosam superavit, et ad solutionem problematum practicorum, necesse est plerumque in relationibus empiricis vel semiempiricis niti.

Antlia Ignis Turbinae Verticalis
Numerus exemplaris: XBC-VTP
Antliae verticales extinguendi ignem longi axis seriei XBC-VTP sunt antliae diffusoriae unius gradus et multigradi, fabricatae secundum recentissimam Normam Nationalem GB6245-2006. Designum etiam emendavimus secundum normam Societatis Protectionis Ignis Civitatum Foederatarum. Praecipue adhibentur ad aquam exstinguendam in petrochemicis, gasis naturalibus, centralibus electricis, textilibus gossypii, portubus, aviatione, horreis, aedificiis altis, aliisque industriis. Etiam adhiberi possunt ad naves, cisternas maritimas, naves extinguendas, aliisque occasionibus alimentationis.
Fluxus rotationalis et irrotationalis.
Fluxus rotatorius dicitur si quaeque particula fluida velocitatem angularem circa centrum massae suae habet.
Figura 2a distributionem velocitatis typicam cum fluxu turbulento ultra limitem rectum ostendit. Ob distributionem velocitatis non uniformem, particula cuius duo axes initialiter perpendiculares sunt deformationem cum parvo gradu rotationis patitur. In Figura 2a, fluxus in circulo...
Via depicta est, velocitate radio directe proportionali. Duo axes particulae in eandem directionem rotantur, ita ut fluxus iterum rotationalis sit.
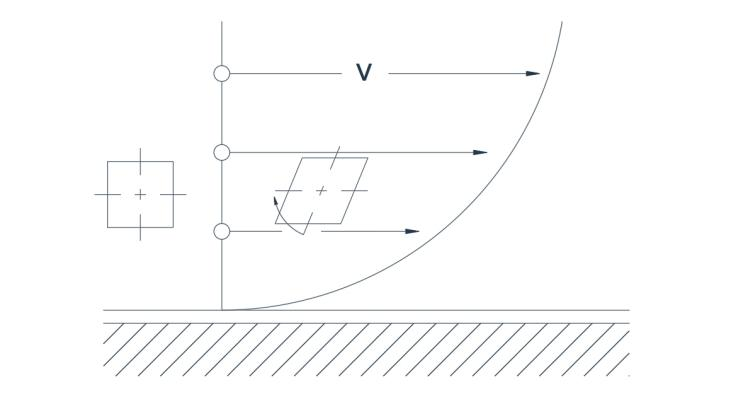
Fig. 2(a) Fluxus rotationis
Ut fluxus irrotationalis sit, distributio velocitatis iuxta limitem rectum uniformis esse debet (Fig. 2b). In casu fluxus in via circulari, demonstrari potest fluxum irrotationalem tantum pertinere dummodo velocitas sit inverse proportionalis radio. Primo aspectu Figurae 3, hoc erroneum videtur, sed examinatio accuratior revelat duos axes in directiones oppositas rotari, ita ut effectus compensans sit, qui orientationem mediam axium producit, quae immutata est ab statu initiali.
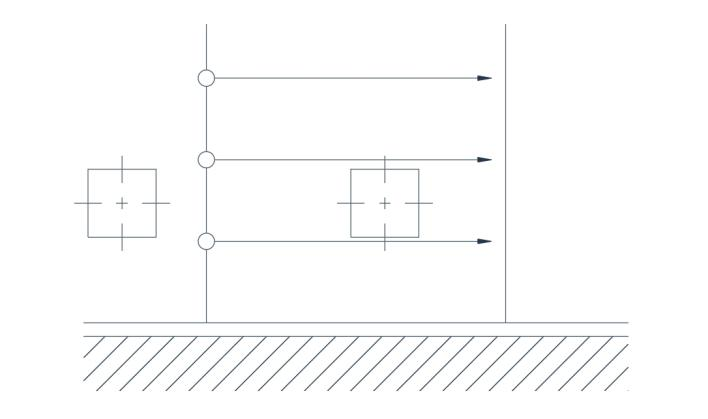
Fig. 2(b) Fluxus irrotationis
Quia omnia fluida viscositatem habent, imum fluidi veri numquam vere irrotatio est, et fluxus laminaris sane valde rotationalis est. Ergo fluxus irrotationalis condicio hypothetica est quae tantum interesse academicum haberet, nisi ob id quod in multis casibus fluxus turbulenti proprietates rotationales tam insignificantes sunt ut neglegi possint. Hoc commodum est quia fluxum irrotationalem per notiones mathematicas hydrodynamicae classicae antea memoratas analysare possibile est.
Antlia Centrifuga Aquae Marinae Destinata
Numerus exemplaris: ASN ASNV
Antliae exemplares ASN et ASNV sunt antliae centrifugae unius gradus, duplici suctione, volutarum involucro diviso, et ad translationem liquidi adhibentur in operibus aquariis, circulatione aeris conditionati, aedificiis, irrigatione, stationibus antliae exhauriendi aquas, stationibus electricis, systematibus aquae industrialibus, systematibus ignis exstinctionis, navibus, aedificiis, et cetera.

Fluxus constans et instabilis.
Fluxus constans dicitur cum condiciones in quolibet puncto constantes sunt respectu temporis. Interpretatio stricta huius definitionis ad conclusionem duceret fluxum turbulentum numquam vere constans fuisse. Attamen, ad praesentem propositum, commodum est motum generalem fluidi tamquam criterium et fluctuationes erraticas cum turbulentia consociatas tamquam vim secundariam tantum considerare. Exemplum manifestum fluxus constans est emissio constans in fistula vel canali aperto.
Corollarium igitur sequitur fluxum instabilem esse cum condiciones variantur respectu temporis. Exemplum fluxus instabilis est fluxus variabilis in fistula vel canali aperto; hoc plerumque est phaenomenon transitorium quod succedit vel sequitur fluxum stabilem. Alia nota...
Exempla naturae magis periodicae sunt motus undarum et motus cyclicus magnarum aquarum corporum in fluxu aestuum.
Pleraque problemata practica in arte hydraulica ad fluxum stabilem pertinent. Hoc felix est, cum variabilis temporis in fluxu instabili analysin magnopere complicat. Proinde, in hoc capitulo, consideratio fluxus instabilis ad pauca exempla relative simplicia restringetur. Interest tamen meminisse nonnulla exempla communia fluxus instabilis ad statum stabilem reduci posse vi principii motus relativi.
Ergo, problema navis per aquam stagnantem moventis, ita reformulari potest ut navis immota sit et aqua in motu sit; unicum criterium similitudinis fluidi est ut velocitas relativa eadem sit. Iterum, motus undarum in aqua alta reduci potest ad...
statum stabilem assumendo observatorem cum undis eadem velocitate progredi.

Antlia Exhauriendi Aquae cum Turbina Verticali Diesel, Multigrada, cum Axe Inline. Hoc genus antliae exhauriendi verticalis praecipue adhibetur ad exhauriendas aquas cloacales vel sordidas, ubi temperaturae inferiores sunt ad 60°C, sed non corrosae, sed cum solidis suspensis (praeter fibras et aream) minus quam 150 mg/L contentis. Antlia exhauriendi verticalis generis VTP in antliis aquariis verticalibus generis VTP est, et, secundum augmentum et collare, oleum tubi ad lubricationem aquae constituitur. Fumus, temperatura infra 60°C adhibitus, grana solida (ut ferrum vetus, arenam subtilem, carbo, etc.) ex cloacis vel aqua sordida continere potest.
Fluxus uniformis et inuniformis.
Fluxus uniformis dicitur cum nulla variatio est in magnitudine et directione vectoris velocitatis ab uno puncto ad alterum secundum cursum fluxus. Ut huic definitioni obsequatur, et area fluxus et velocitas eaedem esse debent in omni sectione transversali. Fluxus non uniformis fit cum vector velocitatis variat cum loco, exemplum typicum est fluxus inter limites convergentes vel divergentes.
Ambae hae condiciones fluxus alternativae communes sunt in hydraulicis canalium apertorum, quamquam stricte loquendo, cum fluxus uniformis semper asymptotice acceditur, status idealis est qui tantum approximatur et numquam re vera attingitur. Notandum est condiciones ad spatium potius quam ad tempus pertinere et ideo in casibus fluxus inclusi (e.g., tubi sub pressione), eas a natura stabili vel instabili fluxus prorsus independentes esse.
Tempus publicationis: Martii XXIX, MMXXIV
 sales@tkflow.com
sales@tkflow.com 
